Tags
biology, brain, Cognition, illusions, Optical illusion, perception, Popular science, science, vision, Visual system, Waterfall
 Humans have an exquisite sense of vision. It’s the primary sense for most of us and our making way of interacting with the world around us. We process the massive amount of visual data generated by sight using trillions of interconnections between billions of neurons spread across half our cerebral cortex. Despite this, our visual system falls prey to illusions, constructing ambiguous interpretations and objects that can’t or don’t exist. How do these illusions work and why do they succeed in fooling us even when we know about them?
Humans have an exquisite sense of vision. It’s the primary sense for most of us and our making way of interacting with the world around us. We process the massive amount of visual data generated by sight using trillions of interconnections between billions of neurons spread across half our cerebral cortex. Despite this, our visual system falls prey to illusions, constructing ambiguous interpretations and objects that can’t or don’t exist. How do these illusions work and why do they succeed in fooling us even when we know about them?
 Figures like MC Escher’s Waterfall and the Penrose triangle are frequently described as impossible. The images exist, so clearly the pictures themselves aren’t “impossible”. The impossibility of these structures comes from our minds attempt to interpret them as two-dimensional projections of three-dimensional structures; that is, we understand the images but think that the objects they depict couldn’t exist. The three-dimensional structures appear to bend back on themselves in ways that violate our intuition of space.
Figures like MC Escher’s Waterfall and the Penrose triangle are frequently described as impossible. The images exist, so clearly the pictures themselves aren’t “impossible”. The impossibility of these structures comes from our minds attempt to interpret them as two-dimensional projections of three-dimensional structures; that is, we understand the images but think that the objects they depict couldn’t exist. The three-dimensional structures appear to bend back on themselves in ways that violate our intuition of space.
 To explain this discrepancy, we need to understand how our visual system constructs a three-dimensional world from what we see. We form images of the world when light strikes the retina, a sheet of light-sensitive cells at the back of our eyes; this creates a flat picture from which we have to reconstruct the world around us. In principle, the image we see could correspond be generated by an infinite number of different worlds. For example, a straight line somewhere in our sight might represent a straight line out in the world, but it might also be a flat surface viewed edge-on — say, a piece of paper seen from the side. In fact, a the paper wouldn’t even have to be rectangular; a circle (or paper of any other shape) viewed edge-on would still look like a straight line. Our visual system uses a set of simple and powerful rules to make sense of the images it gets and to construct a single, coherent world view from them. One such rule is the rule of “generic views”, which simply means that we prefer to interpret what we see as though there were nothing special about our vantage point. If a straight line in your sight was actually a sheet of paper, then a slight shift of view would reveal the paper; in other words, you would have to be quite lucky to have such a perspective of a piece of paper. We tend to process images as though we’re not in such a privileged position, which is why we see straight lines simply as lines and why the Necker cube in the middle looks like a 3-d cube while the flanking images look more like flat surfaces:
To explain this discrepancy, we need to understand how our visual system constructs a three-dimensional world from what we see. We form images of the world when light strikes the retina, a sheet of light-sensitive cells at the back of our eyes; this creates a flat picture from which we have to reconstruct the world around us. In principle, the image we see could correspond be generated by an infinite number of different worlds. For example, a straight line somewhere in our sight might represent a straight line out in the world, but it might also be a flat surface viewed edge-on — say, a piece of paper seen from the side. In fact, a the paper wouldn’t even have to be rectangular; a circle (or paper of any other shape) viewed edge-on would still look like a straight line. Our visual system uses a set of simple and powerful rules to make sense of the images it gets and to construct a single, coherent world view from them. One such rule is the rule of “generic views”, which simply means that we prefer to interpret what we see as though there were nothing special about our vantage point. If a straight line in your sight was actually a sheet of paper, then a slight shift of view would reveal the paper; in other words, you would have to be quite lucky to have such a perspective of a piece of paper. We tend to process images as though we’re not in such a privileged position, which is why we see straight lines simply as lines and why the Necker cube in the middle looks like a 3-d cube while the flanking images look more like flat surfaces:
 The images on the left and right could be cubes, but you would have to be looking at them from a particular angle in order for the parts to overlap so conveniently. Instead, we prefer to see them as flat shapes. The rule of geometric views, together with rules about things like occlusion, the apparent distance between objects, or the interpretation of 2-d curves in 3-d, enables our visual system to construct a three-dimensional interpretation of the flat images cast upon our retina. When applied to images like Escher’s Waterfall or the Penrose Triangle, these rules generate objects that violate our expectations of the physical world. In fact, it’s perfectly possible to build a real, physical object that looks like the Penrose Triangle when viewed from the correct angle, but the rule of generic views prevents us from constructing the correct shape when we see it.
The images on the left and right could be cubes, but you would have to be looking at them from a particular angle in order for the parts to overlap so conveniently. Instead, we prefer to see them as flat shapes. The rule of geometric views, together with rules about things like occlusion, the apparent distance between objects, or the interpretation of 2-d curves in 3-d, enables our visual system to construct a three-dimensional interpretation of the flat images cast upon our retina. When applied to images like Escher’s Waterfall or the Penrose Triangle, these rules generate objects that violate our expectations of the physical world. In fact, it’s perfectly possible to build a real, physical object that looks like the Penrose Triangle when viewed from the correct angle, but the rule of generic views prevents us from constructing the correct shape when we see it.
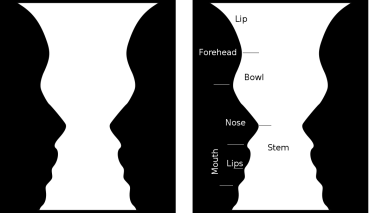
 Figure-ground illusions, such as the Rubin vase or the young/old woman at the top of the post, appear ambiguous because they present equally two valid ways of subdividing the image. Our visual system uses concave curves (areas where a figure curves inwards) to break an image into parts which it then tries to combine into a recognizable object. In these illusions, two different sets of complementary concave curves divide the image into equally recognizable objects; as a result, we switch between different interpretations: a vase or a pair of faces; a young woman or an old one.
Figure-ground illusions, such as the Rubin vase or the young/old woman at the top of the post, appear ambiguous because they present equally two valid ways of subdividing the image. Our visual system uses concave curves (areas where a figure curves inwards) to break an image into parts which it then tries to combine into a recognizable object. In these illusions, two different sets of complementary concave curves divide the image into equally recognizable objects; as a result, we switch between different interpretations: a vase or a pair of faces; a young woman or an old one.
 Many illusions are based on contextual clues confusing our visual system. For example, the two slabs in the image below appear to be different colours but can be seen to be identical by covering up the middle portion of the image (where they meet). Although the two slabs are the same shade of grey, they have opposite gradients around the point where they meet; the top slab gradually gets darker near the intersection while the bottom slab becomes lighter. Our visual system processes these gradients as clues about lighting and interprets them to mean that the top slab is being lit while the lower one is in shadow. Since the two slabs are the same colour and cast the same light onto our eyes, our visual system interprets the one that seems to be in shadow as though it were a lighter shade — which it would have to be in order to look the same colour even though it’s in shadow. If you cover the intersection with your finger or a strip of paper, the misleading gradients disappear and you can see that the two slabs are the same colour.
Many illusions are based on contextual clues confusing our visual system. For example, the two slabs in the image below appear to be different colours but can be seen to be identical by covering up the middle portion of the image (where they meet). Although the two slabs are the same shade of grey, they have opposite gradients around the point where they meet; the top slab gradually gets darker near the intersection while the bottom slab becomes lighter. Our visual system processes these gradients as clues about lighting and interprets them to mean that the top slab is being lit while the lower one is in shadow. Since the two slabs are the same colour and cast the same light onto our eyes, our visual system interprets the one that seems to be in shadow as though it were a lighter shade — which it would have to be in order to look the same colour even though it’s in shadow. If you cover the intersection with your finger or a strip of paper, the misleading gradients disappear and you can see that the two slabs are the same colour.
 Likewise, the Shepard tables use perspective and other contextual clues (such as the legs) to fool our visual system into thinking that two tabletops are different shapes, although measurement will confirm that they are in fact identical.
Likewise, the Shepard tables use perspective and other contextual clues (such as the legs) to fool our visual system into thinking that two tabletops are different shapes, although measurement will confirm that they are in fact identical.
 In completion illusions, such as the Kanizsa triangle, our visual system constructs apparent objects that don’t really exist. Most people viewing this image will see a whiter-than-white triangle, often with distinct edges, although the only things in the picture are the lines and incomplete circles. Researchers have explored a variety of possible explanations for why we perceive illusory contours forming shapes in these images. The underlying figure doesn’t have to be symmetric in order for the illusion to work, as can be seen in the figure on the right:
In completion illusions, such as the Kanizsa triangle, our visual system constructs apparent objects that don’t really exist. Most people viewing this image will see a whiter-than-white triangle, often with distinct edges, although the only things in the picture are the lines and incomplete circles. Researchers have explored a variety of possible explanations for why we perceive illusory contours forming shapes in these images. The underlying figure doesn’t have to be symmetric in order for the illusion to work, as can be seen in the figure on the right:
 Factors like the amount of contrast (i.e., the ratio of black to white) also didn’t provide a satisfactory explanation. Junctions between light and dark or different shades of grey are used by our visual system as clues about where objects meet and how they’re lit. Completion illusions work because we often interpret certain kinds of junctions (those shaped like and L or a T) as evidence of one object occluding another. In the Kanizsa triangle, the (approximately) L-shaped junctions in the Pacman-like circles and the junctions interrupting the lines convince our visual system that a white triangle is floating above the other shapes, blocking portions of them from our sight.
Factors like the amount of contrast (i.e., the ratio of black to white) also didn’t provide a satisfactory explanation. Junctions between light and dark or different shades of grey are used by our visual system as clues about where objects meet and how they’re lit. Completion illusions work because we often interpret certain kinds of junctions (those shaped like and L or a T) as evidence of one object occluding another. In the Kanizsa triangle, the (approximately) L-shaped junctions in the Pacman-like circles and the junctions interrupting the lines convince our visual system that a white triangle is floating above the other shapes, blocking portions of them from our sight.
Illusions work because they represent cases where the rules used by our visual system generate ambiguous or unexpected interpretations of the world around us. Given that the a natural question arises: why would we evolve a set of rules that fails to accurately depict the world around us? The answer to that question can be found in my most recent post on Accumulating Glitches, where I present the case that natural selection has not equipped us with a truthful visual system.
Refs
Hoffman, Donald Visual Intelligence. New York: W.W. Norton & Company (1998).
Adelson, E.H. Lightness Perception and Lightness Illusions. In The New Cognitive Neurosciences, 2nd ed., M. Gazzaniga, ed. Cambridge, MA: MIT Press, (2000).
Eagleman, D. (2001). TIMELINE: Visual illusions and neurobiology Nature Reviews Neuroscience, 2 (12), 920-926 DOI: 10.1038/35104092

M.C. Escher and Cuthulu…aren’t they the same guy?
Reblogged this on Oyia Brown.
Pingback: Found while foraging (July 3, 2013) | Inspiring Science